가정해 보겠습니다. 밥이 앨리스에게 메시지를 보내고 싶어하지만, 메시지가 비밀로 유지될 필요는 없지만, 앨리스가 그 메시지가 실제로 자신으로부터 온 것임을 확실히 알기를 원합니다.
▪ 인증
• 사용자가 밥의 공개 키를 사용하여 밥의 암호문에서 평문을 성공적으로 복구할 수 있다면, 이는 밥만이 평문을 암호화할 수 있었음을 나타내므로 인증을 제공합니다.
▪. 인증 또는 데이터 무결성
• 밥만이 평문을 밥의 비밀 키로 암호화할 수 있기 때문에 밥 외에는 아무도 평문을 수정할 수 없습니다.
❖ 여기서 전체 메시지가 암호화되는데, 이는 저자와 내용을 모두 검증하지만, 많은 저장 공간과 추가 처리 비용을 요구합니다.
❖. 동일한 결과를 보다 효율적으로 달성하는 더 나은 방법은 문서의 함수인 작은 비트 블록, 즉 인증자를 암호화하는 것입니다.
▪. 인증자가 발신자의 비공개 키로 암호화되면, 이는 출처, 내용 및 순서를 검증하는 서명으로 기능합니다.
▪ . SHA-1과 같은 안전한 해시 코드가 이 기능을 수행할 수 있습니다.
▪. 디지털 서명은 기밀성을 제공하지 않는다는 점을 강조하는 것이 중요합니다. 즉, 전송되는 메시지는 변경으로부터 안전하지만 도청으로부터는 안전하지 않습니다.
암호는 누구나하지만 복호화는 한명만 할수있어야한다는것 인증은 자기자신만 할수있어야한다. 확인을 할수는 있지만 풀어보는것은 프라이빗 키로만한다.
공개 키 요구 사항
❖ 계산적으로 쉽게 키 쌍(공개 키 PUb, 비공개 키 PRb)을 생성할 수 있어야 합니다.
❖ 공개 키를 알고 있는 송신자가 메시지를 암호화하기 쉬워야 합니다: C=E(PUb,M)
❖ 비공개 키를 알고 있는 수신자가 암호문을 복호화하기 쉬워야 합니다: M=D(PRb,C)
❖ 공개 키 PUb를 알고 있는 상대가 비공개 키, PRb를 결정하는 것이 계산적으로 불가능해야 합니다.
❖ 공개 키, PUb와 암호문 C를 알고 있는 상대가 원본 메시지 M을 복구하는 것이 계산적으로 불가능해야 합니다.
❖ 두 관련 키 중 하나를 암호화에 사용할 수 있고, 다른 하나를 복호화에 사용할 수 있는 경우 유용합니다.
공개 키 알고리즘
❖ 디피-헬만 키 교환 알고리즘
▪ 1976년에 개발됨
▪ 비밀 키 교환만 가능
❖ RSA (리베스트, 샤미르, 애들먼)
▪ 1977년에 개발됨
▪ 유일하게 널리 인정받는 공개 키 암호화 알고리즘
▪ 평문과 암호문이 어떤 n에 대해 0부터 n – 1 사이의 정수인 블록 암호
▪ 현재는 1024비트 키 크기(약 300개의 십진수)가 충분히 강력한 것으로 간주됨.
❖ 타원 곡선 암호학 (ECC)
▪ 새롭지만, RSA와 같은 보안성을 제공하지만 키의 크기가 훨씬 작음
▪ ECC에 대한 신뢰도는 아직 RSA만큼 높지 않음
❖ 디지털 서명 표준 (DSS)
▪ NIST가 FIPS PUB 186을 발행함
▪ SHA-1을 사용하는 디지털 서명 기능만 제공
디피 헬만은 이산수학 mod연산을 통한 교환 알고리즘이다.

응용 프로그램: 공개 키 인증서
❖ 키 분배 문제를 해결하기 위한 두 가지 구별된 측면
▪ 공개 키의 진위성
• 왜? 공개 키가 공개적이지만 문제는 지정된 사용자의 공개 키를 실제로 가지고 있는지, 아니면 위조품이 아닌지를 아는 것입니다.
• 해결책: 공개 키 인증서는 공개 키와 키 소유자의 사용자 ID를 포함하며, 전체 블록이 신뢰할 수 있는 제3자에 의해 서명됩니다. 사용자는 자신의 공개 키를 안전한 방법으로 권한에 제시하고 인증서를 받을 수 있습니다. 그런 다음 사용자는 인증서를 공개할 수 있습니다.
▪ 비밀 키를 분배하기 위한 공개 키 암호화 사용
키 분배 문제를 해결하기 위한 두 가지 구별된 측면(계속)
▪ 공개 키의 진위성
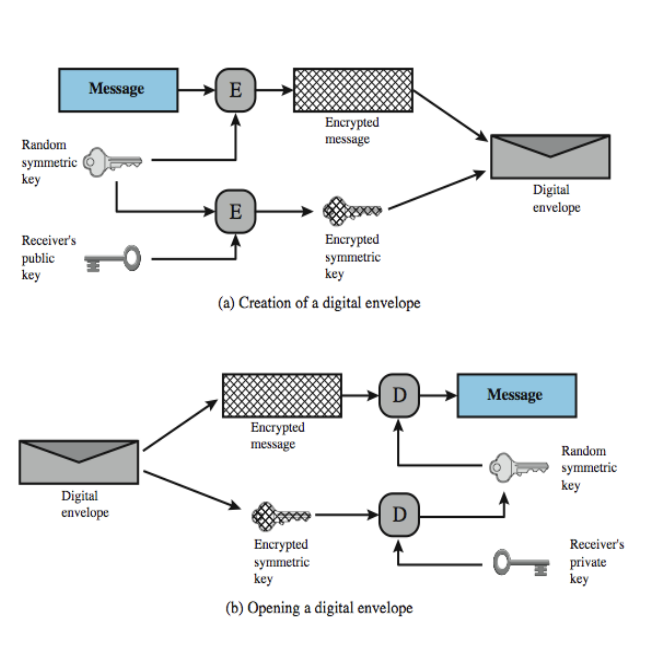
▪ 비밀 키를 분배하기 위한 공개 키 암호화 사용: 디지털 봉투
• 발신자와 수신자가 동일한 비밀 키를 사전에 준비하지 않고도 메시지를 보호할 수 있습니다.
• 밥이 앨리스에게 기밀 메시지를 보내고 싶지만 그들은 대칭 비밀 키를 공유하지 않는다고 가정해 봅시다. 밥은 다음과 같은 작업을 합니다:
메시지 준비
일회용 일반 세션 키를 사용한 일반 암호화로 해당 메시지를 암호화합니다.
앨리스의 공개 키를 사용한 공개 키 암호화로 세션 키를 암호화합니다.
암호화된 세션 키를 메시지에 첨부하여 앨리스에게 보냅니다.

랜덤 숫자
❖ 랜덤 숫자는 다양한 네트워크 보안 애플리케이션에서 암호화 사용에 있어 중요한 역할을 합니다. 예를 들어, 공개 키 알고리즘, 스트림 암호의 스트림 키, 임시 세션 키 및 키 분배 시나리오에서의 키 생성과 같은 경우에 있습니다.
❖ 요구 사항:
▪ 무작위성
• 균일 분포와 독립성에 대한 통계적 검정에 기반
• 균일 분포: 시퀀스 내의 숫자 빈도는 균일하거나 비슷해야 합니다.
• 독립성: 시퀀스의 다른 값에서 특정 값을 얻을 수 없어야 합니다.
▪ 예측 불가능성
• 연속된 값이 이전의 것과 관련되지 않아야 함
• 진정으로 무작위적인 숫자에 대해 분명히 참입니다.
▪ “진정한” 무작위 시퀀스에서는 각 숫자가 시퀀스 내의 다른 숫자와 통계적으로 독립적이므로 예측할 수 없습니다.
❖ 그러나, 진정한 무작위 숫자는 항상 사용되는 것은 아니며, 대신 어떤 알고리즘에 의해 생성된 숫자의 시퀀스가 무작위처럼 보입니다. 종종 알고리즘 기술을 사용하여 의사랜덤 숫자를 생성합니다.
▪ 알고리즘이 좋으면, 결과적인 시퀀스는 많은 합리적인 무작위성 검정을 통과할 것입니다.
▪ 이러한 숫자는 통계적 무작위성 검정을 만족하지만 예측 가능할 수 있는 의사랜덤 숫자로 불립니다.
그 알고리즘중 하나

의사 랜덤 숫자 생성기 (PNRG)
❖ 구현 방법
▪ 선형 합동 방법
• 가장 일반적으로 사용됩니다.
• 시퀀스에서의 출력은 계수 a와 b에 따라 주기성을 가집니다.
▪ Blum Blum Shub (BBS)
• 제곱된 중복 합동을 사용하는 의사랜덤 숫자 생성기가 0과 1의 비트 스트림을 생성합니다.
▪ ANSI X9.17 PNRG
• 비교적 암호학적으로 안전합니다.
• 두 개의 DES 키와 세 개의 3DES가 필요하며, 처리량이 많다는 것이 단점입니다.
DTi: i번째 랜덤 숫자 생성시의 날짜와 시간 정보 (64 비트)
Vi: i번째 랜덤 숫자 생성을 위한 시드 값 (64 비트)
Ri: i번째 랜덤 숫자 (64 비트)
K1, K2: 3DES 키
EDE: 3DES
'정보보안' 카테고리의 다른 글
| 정보보안 - Database Security (0) | 2024.03.25 |
|---|---|
| 정보보안 - Access Control (0) | 2024.03.25 |
| 정보보안 - User Authentication (1) | 2024.03.18 |
| 정보보안 - Cryptographic Tools (0) | 2024.03.11 |
| 정보보안 - Computer Security Overview (1) | 2024.03.06 |


